ITSatellite

CE, LE 계산

, , ,

관측값 즉, 지상기준점과 측정점의 차이에 대해 CE 및 LE 결과를 내기 위해 구현을 하게 되었고 참고자료를 바탕으로 정리하였습니다.

소스 코드는 CE, LE 계산 사이트에 있습니다.

CE(Circular Error)

  • X, Y 축의 값에 대한 2차원 오차를 측정합니다.
  • 원형오차라고 부르며, CE 50, CE 90, CE 95 등의 형식으로 표현합니다.
  • 예) CE90 5m는 오차들이 실제 값에서 5m 반경 안에 90% 있음을 나타냄.

CE 90 계산

1) 관측값 평균이 0일 경우

  • CE_XX = R * 𝜎𝑚𝑎𝑥
  1. 2x2 공분산 행렬을 계산하고, 공분산 행렬에 대해 고유값(Eigenvalue) 계산
  2. 최소, 최대 고유값에 대해 제곱근으로 𝜎𝑚𝑖𝑛, 𝜎𝑚𝑎𝑥 값을 구함
    • 예) MATLAB은 eig(A) 함수를 사용
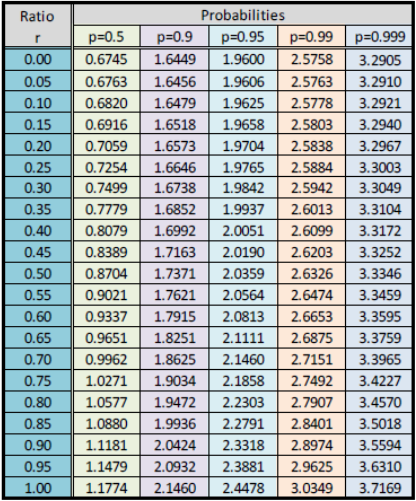
  3. r = 𝜎𝑚𝑖𝑛/𝜎𝑚𝑎𝑥, p=90/100 두 개의 값과 아래 표의 값을 통해 선형 보간하여 확률 계수 R을 구함
    • 예) r = 0.509, p = 0.9 일 때, R = 0.041/0.05 * 1.7371 + 0.009/0.05 * 1.7621 = 1.7416
  4. 확률 계수와 𝜎𝑚𝑎𝑥를 곱함

2) 관측값 평균이 0이 아닐 경우

  1. X, Y 축에 대해 각각 공분산 값을 구하고 2x2 공분산 행렬을 계산
  2. i 수만큼 위의 수식으로 2x1(X, Y)의 Si를 계산
  3. Si의 크기를 가장 작은 것부터 가장 큰 것 순으로 정렬(크기는 아래 수식과 같음)

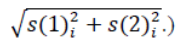
  1. RExx는 xx% 가장 큰 크기, RE*xx는 다음으로 큰 크기를 지정.
  2. CE_XX 계산은 아래 수식으로 계산.

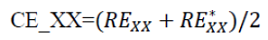
LE(Linear Error)

  • Z 축(고도)에 대한 오차를 측정합니다.
  • 지형의 수직 정확도를 측정합니다.(TIN, DEM, DSM 등)
  • 선형오차라고 부르며, LE 50, LE 90, LE 95 등의 형식으로 표현합니다.

LE 90 계산

1) 관측값 평균이 0일 경우

  • LE_XX = P(확률계수) * 𝜎𝑧 (표준편차)
  1. 관측값에 대한 표준편차를 구함
  2. 다음의 표에서 p=90/100(0.90)에 대한 확률 계수인 1.6449를 구함
  3. 표준편차와 확률 계수를 곱함
  • LE_90 = 1.6449 * (표준편차)

2) 관측값 평균이 0이 아닐 경우

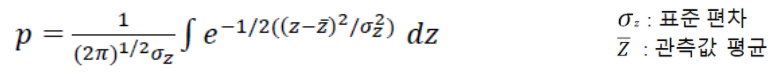
  1. 기준점과 측정점을 통해 표준편차와 평균을 구함
  2. 위의 식(누적분포함수)에서 p 값을 계산
  3. p 값에 대해 오차 역함수(Inverse Error Function)를 구함
  4. 다음의 식을 통해 LE를 계산

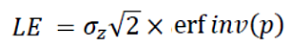
참고내용

1) 분산(Variance)

  • 관측값에 대한 분산

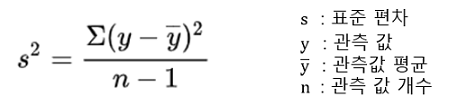
2) 공분산(Covariance)

  • 관측값에 대한 공분산

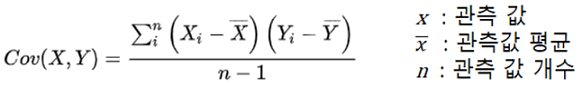
3) 공분산 행렬

  • 두 개의 확률 변수의 공분산 행렬은 각 변수 쌍에 대해 계산된 공분산 값으로 구성된 행렬

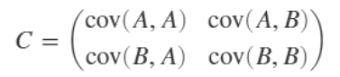
4) 표준편차(Standard Deviation)

  • 관측값에 대한 표준편차

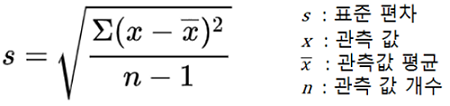
참고자료

  • Computation of scalar accuracy metrics LE, CE, and SE as both predictive and samplebased statistics (NGA)
  • Geopositional Statistical Methods (NASA)
Share